תוֹכֶן

• צעדים

משוואה טריגונומטרית מכילה פונקציה טריגונומטרית אחת או יותר של המשתנה "x" (או כל משתנה אחר). פתרון משוואה טריגונומטרית הוא מציאת ערך כזה "x" העונה על הפונקציות (ים) והמשוואה כולה.

• פתרונות למשוואות טריגונומטריות מתבטאים במעלות או ברדיאנים. דוגמאות:

x = π / 3; x = 5π / 6; x = 3π / 2; x = 45 מעלות; x = 37.12 מעלות; x = 178.37 מעלות.

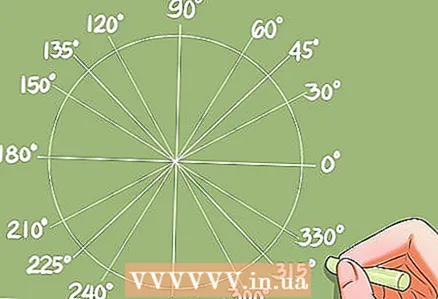
• הערה: ערכי הפונקציות הטריגונומטריות מזוויות, המתבטאות ברדיאנים, וזוויות, המתבטאות במעלות, שוות. מעגל טריגונומטרי בעל רדיוס שווה לאחד משמש לתיאור פונקציות טריגונומטריות, כמו גם לבדיקת נכונות הפתרון של המשוואות הטריגונומטריות הבסיסיות ואי -השוויון.
• דוגמאות למשוואות טריגונומטריות:
  • חטא x + חטא 2x = 1/2; tg x + ctg x = 1.732;
  • cos 3x + sin 2x = cos x; 2 שניות 2x + cos x = 1.

1. מעגל טריגונומטרי עם רדיוס של אחד (מעגל יחידה).
   • זהו מעגל עם רדיוס השווה לאחד ומרכז בנקודה O. מעגל היחידה מתאר 4 פונקציות טריגונומטריות בסיסיות של המשתנה "x", כאשר "x" הוא הזווית הנמדדת מהכיוון החיובי של ציר ה- X נגד כיוון השעון.
   • אם "x" הוא זווית כלשהי במעגל היחידה, אז:
   • הציר האופקי OAx מגדיר את הפונקציה F (x) = cos x.
   • הציר האנכי OBy מגדיר את הפונקציה F (x) = sin x.
   • הציר האנכי AT מגדיר את הפונקציה F (x) = tan x.
   • הציר האופקי BU מגדיר את הפונקציה F (x) = ctg x.

• מעגל היחידה משמש גם לפתרון משוואות טריגונומטריות בסיסיות ואי -שוויון (נבחנות בו מיקומים שונים של "x").

צעדים

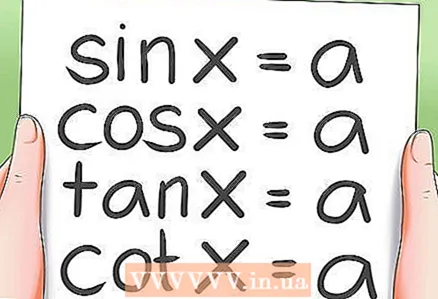1. 1 הרעיון של פתרון משוואות טריגונומטריות.
   • כדי לפתור משוואה טריגונומטרית, המר אותה למשוואה טריגונומטרית בסיסית אחת או יותר. פתרון משוואה טריגונומטרית מגיע בסופו של דבר לפתרון ארבע משוואות טריגונומטריות בסיסיות.
2. 2 פתרון משוואות טריגונומטריות בסיסיות.
   • ישנם 4 סוגים של משוואות טריגונומטריות בסיסיות:
   • חטא x = a; כי x = א
   • tg x = a; ctg x = a
   • פתרון משוואות טריגונומטריות בסיסיות כולל הסתכלות על מיקומי ה- x השונים במעגל היחידה ושימוש בטבלת המרות (או מחשבון).
   • דוגמה 1. כין x = 0.866. באמצעות טבלת המרות (או מחשבון) מתקבלת התשובה: x = π / 3. מעגל היחידה נותן תשובה נוספת: 2π / 3. זכור: כל הפונקציות הטריגונומטריות הינן תקופתיות, כלומר ערכיהם חוזרים על עצמם. לדוגמה, המחזוריות של sin x ו- cos x היא 2πn, והמחזוריות של tg x ו- ctg x היא πn. לכן התשובה כתובה כך:
   • x1 = π / 3 + 2πn; x2 = 2π / 3 + 2πn.
   • דוגמה 2. cos x = -1/2. באמצעות טבלת המרות (או מחשבון) מתקבלת התשובה: x = 2π / 3. מעגל היחידה נותן תשובה נוספת: -2π / 3.
   • x1 = 2π / 3 + 2π; x2 = -2π / 3 + 2π.
   • דוגמה 3. tg (x - π / 4) = 0.
   • תשובה: x = π / 4 + πn.
   • דוגמה 4. ctg 2x = 1.732.
   • תשובה: x = π / 12 + πn.
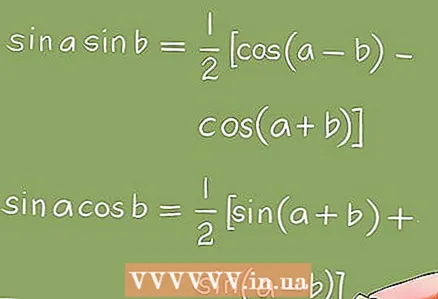3. 3 טרנספורמציות המשמשות לפתרון משוואות טריגונומטריות.
   • כדי להפוך משוואות טריגונומטריות משתמשים בתמורות אלגבריות (פקטורטיזציה, הפחתת מונחים הומוגניים וכו ') וזהויות טריגונומטריות.
   • דוגמה 5. באמצעות זהויות טריגונומטריות, המשוואה sin x + sin 2x + sin 3x = 0 הופכת למשוואה 4cos x * sin (3x / 2) * cos (x / 2) = 0. לכן, עליך לפתור את המשוואות הטריגונומטריות הבסיסיות הבאות: cos x = 0; חטא (3x / 2) = 0; cos (x / 2) = 0.
     
     
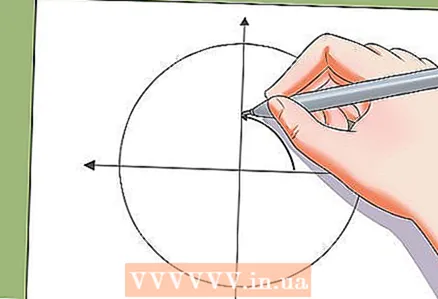
4. 4 מציאת זוויות מערכים ידועים של פונקציות.
   • לפני למידת שיטות לפתרון משוואות טריגונומטריות, עליך ללמוד כיצד למצוא זוויות מערכים ידועים של פונקציות. ניתן לעשות זאת באמצעות טבלת המרות או מחשבון.
   • דוגמה: cos x = 0.732. המחשבון ייתן את התשובה x = 42.95 מעלות. מעגל היחידה ייתן זוויות נוספות, שהקוסינוס שלהן הוא גם 0.732.
5. 5 הניחו את הפתרון בצד במעגל היחידה.
   • אתה יכול לדחות את הפתרונות למשוואה הטריגונומטרית במעגל היחידה. הפתרונות של המשוואה הטריגונומטרית במעגל היחידה הם קודקודים של מצולע רגיל.
   • דוגמה: הפתרונות x = π / 3 + πn / 2 במעגל היחידה הם קודקודים של ריבוע.
   • דוגמה: הפתרונות x = π / 4 + πn / 3 במעגל היחידה מייצגים את הקודקודים של משושה רגיל.
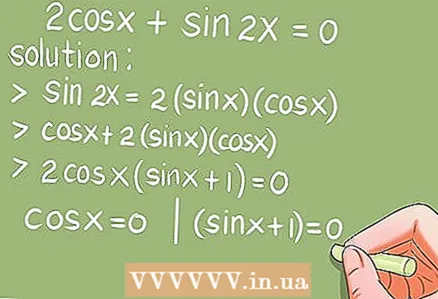6. 6 שיטות לפתרון משוואות טריגונומטריות.
   • אם משוואת טריג נתונה מכילה רק פונקציית טריג אחת, פתר את המשוואה כמשוואת הטריג הבסיסית.אם משוואה נתונה כוללת שתי פונקציות טריגונומטריות או יותר, הרי שישנן 2 שיטות לפתרון משוואה כזו (בהתאם לאפשרות השינוי שלה).
     • שיטה 1.
   • המר את המשוואה הזו למשוואה בצורה: f (x) * g (x) * h (x) = 0, כאשר f (x), g (x), h (x) הן המשוואות הטריגונומטריות הבסיסיות.
     
     
   • דוגמה 6.2cos x + sin 2x = 0. (0 x 2π)
   • פִּתָרוֹן. באמצעות נוסחת הזווית הכפולה sin 2x = 2 * sin x * cos x, החליף את החטא 2x.
   • 2cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. עכשיו פתרו את שתי המשוואות הטריגונומטריות הבסיסיות: cos x = 0 ו- (sin x + 1) = 0.
   • דוגמה 7. cos x + cos 2x + cos 3x = 0. (0 x 2π)
   • פתרון: באמצעות זהויות טריגונומטריות, הפוך משוואה זו למשוואה של הצורה: cos 2x (2cos x + 1) = 0. עכשיו פתור את שתי המשוואות הטריגונומטריות הבסיסיות: cos 2x = 0 ו- (2cos x + 1) = 0.
   • דוגמה 8. sin x - sin 3x = cos 2x. (0 x 2π)
   • פתרון: באמצעות זהויות טריגונומטריות, הפוך משוואה זו למשוואה בצורה: -קוס 2x * (2sin x + 1) = 0. עכשיו פתור את שתי המשוואות הטריגונומטריות הבסיסיות: cos 2x = 0 ו- (2sin x + 1) = 0.
     • שיטה 2.
   • המר את המשוואה הטריגונומטרית הנתונה למשוואה המכילה פונקציה טריגונומטרית אחת בלבד. לאחר מכן החלף את הפונקציה הטריגונומטרית בכמה לא ידועים, למשל t (sin x = t; cos x = t; cos 2x = t, tg x = t; tg (x / 2) = t, וכו ').
   • דוגמה 9.3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2π).
   • פִּתָרוֹן. במשוואה זו, החלף (cos ^ 2 x) ב- (1 - sin ^ 2 x) (לפי זהות). המשוואה שהתהפכה היא:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. החלף sin x ב- t. המשוואה כעת נראית כך: 5t ^ 2 - 4t - 9 = 0. זו משוואה ריבועית עם שני שורשים: t1 = -1 ו- t2 = 9/5. השורש השני t2 אינו מספק את טווח הערכים של הפונקציה (-1 sin x 1). כעת תחליטו: t = sin x = -1; x = 3π / 2.
   • דוגמה 10. tg x + 2 tg ^ 2 x = ctg x + 2
   • פִּתָרוֹן. החלף tg x ב- t. כתוב מחדש את המשוואה המקורית כדלקמן: (2t + 1) (t ^ 2 - 1) = 0. כעת מצא t ולאחר מכן מצא x עבור t = tg x.
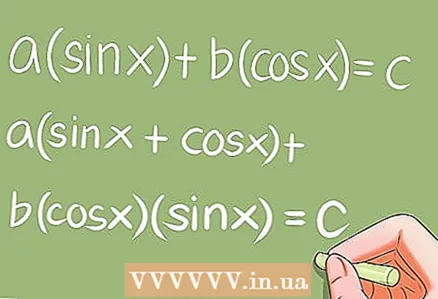7. 7 משוואות טריגונומטריות מיוחדות.
   • ישנן מספר משוואות טריגונומטריות מיוחדות הדורשות טרנספורמציות ספציפיות. דוגמאות:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
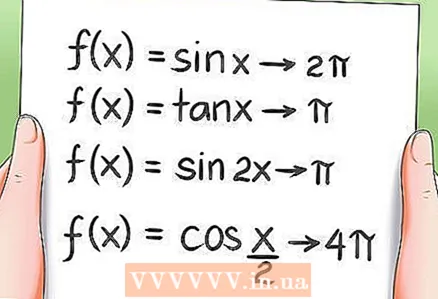8. 8 מחזוריות של פונקציות טריגונומטריות.
   • כפי שצוין קודם לכן, כל הפונקציות הטריגונומטריות הן תקופתיות, כלומר ערכיהם חוזרים על עצמם לאחר תקופה מסוימת. דוגמאות:
     • תקופת הפונקציה f (x) = sin x היא 2π.
     • תקופת הפונקציה f (x) = tan x שווה ל- π.
     • תקופת הפונקציה f (x) = sin 2x היא π.
     • תקופת הפונקציה f (x) = cos (x / 2) היא 4π.
   • אם התקופה מצוינת בבעיה, חשב את הערך "x" בתוך תקופה זו.
   • הערה: פתרון משוואות טריגונומטריות היא משימה לא פשוטה ולעתים קרובות מובילה לשגיאות. אז בדוק היטב את התשובות שלך. לשם כך, ניתן להשתמש במחשבון גרפים כדי לתוות את המשוואה הנתונה R (x) = 0. במקרים כאלה, הפתרונות יוצגו כשברים עשרוניים (כלומר, π מוחלף ב- 3.14).