תוֹכֶן

• לדרוך

משוואה טריגונומטרית היא משוואה עם פונקציה טריגונומטרית אחת או יותר של העקומה הטריגונומטרית המשתנה. פתרון ל- x פירושו מציאת הערכים של העקומות הטריגונומטריות שתפקודיהם הטריגונומטריים גורמים לנכונה של המשוואה הטריגונומטרית.

• התשובות, או הערכים, של עקומות הפתרון באות לידי ביטוי במעלות או ברדיאנים. דוגמאות:

x = Pi / 3; x = 5Pi / 6; x = 3Pi / 2; x = 45 מעלות; x = 37.12 מעלות; x = 178.37 מעלות

• הערה: במעגל היחידה, הפונקציות הטריגונומטריות של כל עקומה שוות לפונקציות הטריגונומטריות של הזווית המתאימה. מעגל היחידה מגדיר את כל הפונקציות הטריגונומטריות של העקומה המשתנה x. הוא משמש גם כהוכחה בפתרון משוואות ואי-שוויונות טריגונומטריים בסיסיים.
• דוגמאות למשוואות טריגונומטריות:
  • חטא x + חטא 2x = 1/2; שזוף x + מיטת תינוק x = 1.732;
  • cos 3x + sin 2x = cos x; 2sin 2x + cos x = 1.

1. מעגל היחידה.
   • זהו מעגל עם רדיוס = 1, כאשר O הוא המקור. מעגל היחידה מגדיר 4 פונקציות טריגונומטריות עיקריות של העקומה המשתנה x, המעגלת אותו נגד כיוון השעון.
   • כאשר העקומה עם הערך x משתנה במעגל היחידה, ואז היא מחזיקה:
   • הציר האופקי OAx מגדיר את הפונקציה הטריגונומטרית f (x) = cos x.
   • הציר האנכי OBy מגדיר את הפונקציה הטריגונומטרית f (x) = sin x.
   • הציר האנכי AT מגדיר את הפונקציה הטריגונומטרית f (x) = שיזוף x.
   • הציר האופקי BU מגדיר את הפונקציה הטריגונומטרית f (x) = מיטת x.

• מעגל היחידה משמש גם לפתרון משוואות טריגונומטריות בסיסיות ואי-שוויון טריגונומטרי סטנדרטי על ידי התחשבות במיקומים השונים של העקומה x במעגל.

לדרוך

1. הבן את שיטת הפתרון.
   • כדי לפתור משוואה טריגונומטרית אתה ממיר אותה למשוואה טריגונומטרית בסיסית אחת או יותר. פתרון משוואות טריגונומטריות גורם בסופו של דבר לפתרון 4 משוואות טריגונומטריות בסיסיות.
2. דע כיצד לפתור משוואות טריגונומטריות בסיסיות.
   • ישנן 4 משוואות טריגונומטריות בסיסיות:
   • חטא x = a; cos x = a
   • שזוף x = a; מיטת תינוק x = א
   • ניתן לפתור את המשוואות הטריגונומטריות הבסיסיות על ידי לימוד המיקומים השונים של העקומה x במעגל הטריגונומטרי ובאמצעות טבלת המרה טריגונומטרית (או מחשבון). כדי להבין באופן מלא כיצד לפתור משוואות טריגונומטריות בסיסיות ודומות להם, קרא את הספר הבא: "טריגונומטריה: פתרון משוואות ואי-שוויונות טריגונומטריות" (ספר אלקטרוני של אמזון 2010).
   • דוגמה 1. לפתור את החטא x = 0.866. טבלת ההמרות (או המחשבון) נותנת את התשובה: x = Pi / 3. המעגל הטריגונומטרי נותן עקומה נוספת (2Pi / 3) עם אותו ערך לסינוס (0.866). המעגל הטריגונומטרי מספק גם אינסוף תשובות הנקראות תשובות מורחבות.
   • x1 = Pi / 3 + 2k.Pi ו- x2 = 2Pi / 3. (תשובות בתוך תקופה (0, 2Pi))
   • x1 = Pi / 3 + 2k Pi, ו- x2 = 2Pi / 3 + 2k Pi. (תשובות מפורטות).
   • דוגמה 2. פתור: cos x = -1/2. מחשבונים נותנים x = 2 Pi / 3. המעגל הטריגונומטרי גם נותן x = -2Pi / 3.
   • x1 = 2Pi / 3 + 2k.Pi, ו- x2 = - 2Pi / 3. (תשובות לתקופה (0, 2Pi))
   • x1 = 2Pi / 3 + 2k Pi, ו- x2 = -2Pi / 3 + 2k.Pi. (תשובות מורחבות)
   • דוגמה 3. לפתור: שזוף (x - Pi / 4) = 0.
   • x = Pi / 4; (תשובה)
   • x = Pi / 4 + k Pi; (תשובה מורחבת)
   • דוגמה 4. לפתור: מיטת תינוק 2x = 1.732. המחשבונים והמעגל הטריגונומטרי נותנים:
   • x = Pi / 12; (תשובה)
   • x = Pi / 12 + k Pi; (תשובות מורחבות)
3. למדו את התמורות המשמשות לפתרון משוואות טריגונומטריות.
   • כדי להמיר משוואה טריגונומטרית נתונה למשוואות טריגונומטריות סטנדרטיות, השתמש בהמרות אלגבריות סטנדרטיות (פקטוריזציה, גורם משותף, פולינומים ...), הגדרות ותכונות של פונקציות טריגונומטריות וזהויות טריגונומטריות. ישנם כ- 31, 14 מהם זהויות טריגונומטריות, בין 19 ל- 31, הנקראות גם זהויות טרנספורמציה, מכיוון שהן משמשות להמרה של משוואות טריגונומטריות. ראה את הספר הנ"ל.
   • דוגמה 5: ניתן להמיר את המשוואה הטריגונומטרית: sin x + sin 2x + sin 3x = 0 לתוצר של משוואות טריגונומטריות בסיסיות תוך שימוש בזהויות טריגונומטריות: 4cos x * sin (3x / 2) * cos (x / 2) = 0. המשוואות הטריגונומטריות הבסיסיות לפתרון הן: cos x = 0; חטא (3x / 2) = 0; ו- cos (x / 2) = 0.
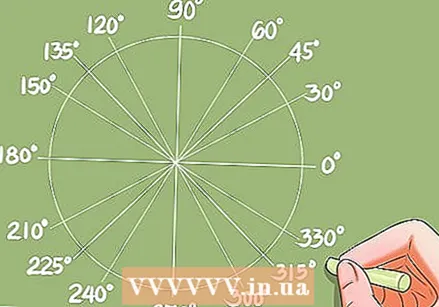4. מצא את העקומות שבגינן ידועות הפונקציות הטריגונומטריות.
   • לפני שתוכל ללמוד לפתור משוואות טריגונומטריות, עליך לדעת למצוא במהירות את העקומות שעבורן ידועות הפונקציות הטריגונומטריות. ניתן לקבוע את ערכי ההמרה של עקומות (או זוויות) באמצעות טבלאות טריגונומטריות או המחשבון.
   • דוגמה: פתר עבור cos x = 0.732. המחשבון נותן את הפתרון x = 42.95 מעלות. מעגל היחידה נותן עקומות אחרות עם אותו ערך עבור הקוסינוס.
5. צייר את קשת התשובה על מעגל היחידה.
   • ניתן ליצור גרף להמחשת הפיתרון במעגל היחידה. נקודות הסיום של העקומות הללו הן מצולעים רגילים במעגל הטריגונומטרי. כמה דוגמאות:
   • נקודות הקצה של העקומה x = Pi / 3 + k. Pi / 2 הוא ריבוע על מעגל היחידה.
   • העקומות של x = Pi / 4 + k.Pi / 3 מיוצגות על ידי הקואורדינטות של משושה במעגל היחידה.
6. למד כיצד לפתור משוואות טריגונומטריות.
   • אם המשוואה הטריגונומטרית הנתונה מכילה פונקציה טריגונומטרית אחת בלבד, פתר אותה כמשוואה טריגונומטרית סטנדרטית. אם המשוואה הנתונה מכילה שתי פונקציות טריגונומטריות או יותר, ישנן שתי שיטות פתרון, בהתאם לאפשרויות להמרת המשוואה.
     • א. שיטה 1.
   • המירו את המשוואה הטריגונומטרית לתוצר מהצורה: f (x) .g (x) = 0 או f (x) .g (x) .h (x) = 0, כאשר f (x), g (x) ו- h (x) הן משוואות טריגונומטריות בסיסיות.
   • דוגמה 6. לפתור: 2cos x + sin 2x = 0. (0 x 2Pi)
   • פִּתָרוֹן. החלף את החטא 2x במשוואה בעזרת הזהות: sin 2x = 2 * sin x * cos x.
   • cos x + 2 * sin x * cos x = 2cos x * (sin x + 1) = 0. ואז לפתור 2 פונקציות טריגונומטריות סטנדרטיות: cos x = 0 ו- (sin x + 1) = 0.
   • דוגמה 7. פתור: cos x + cos 2x + cos 3x = 0. (0 x 2Pi)
   • פתרון: המירו זאת למוצר תוך שימוש בזהויות הטריגונומטריות: cos 2x (2cos x + 1) = 0. פתרו כעת את 2 המשוואות הטריגונומטריות הבסיסיות: cos 2x = 0 ו- (2cos x + 1) = 0.
   • דוגמה 8. פתור: sin x - sin 3x = cos 2x. (0 x 2Pi)
   • פתרון: המירו זאת למוצר, תוך שימוש בזהויות הטריגונומטריות: -cos 2x * (2sin x + 1) = 0. כעת פתרו את 2 המשוואות הטריגונומטריות הבסיסיות: cos 2x = 0, ו- (2sin x + 1) = 0.
     • ב 'גישה 2.
   • ממיר את משוואת הטריג למשוואת טריג עם פונקציית טריג ייחודית אחת בלבד כמשתנה. יש כמה טיפים כיצד לבחור משתנה מתאים. המשתנים הנפוצים הם: sin x = t; cos x = t; cos 2x = t, שזוף x = t ושזוף (x / 2) = t.
   • דוגמה 9. פתור: 3sin ^ 2 x - 2cos ^ 2 x = 4sin x + 7 (0 x 2Pi).
   • פִּתָרוֹן. במשוואה, החלף (cos ^ 2x) ב- (1 - sin ^ 2x) ופשט את המשוואה:
   • 3sin ^ 2 x - 2 + 2sin ^ 2 x - 4sin x - 7 = 0. עכשיו השתמש ב- sin x = t. המשוואה הופכת ל: 5t ^ 2 - 4t - 9 = 0. זו משוואה ריבועית עם 2 שורשים: t1 = -1 ו- t2 = 9/5. אנו יכולים לדחות את ה- t2 השני, מכיוון ש> 1. נפתור כעת: t = sin = -1 -> x = 3Pi / 2.
   • דוגמה 10. לפתור: שיזוף x + 2 שזוף ^ 2 x = עריסה x + 2.
   • פִּתָרוֹן. השתמש בשיזוף x = t. המר את המשוואה הנתונה למשוואה עם t כמשתנה: (2t + 1) (t ^ 2 - 1) = 0. פתר את t ממוצר זה, ואז פתר את המשוואה הטריגונומטרית הסטנדרטית שזוף x = t עבור x.
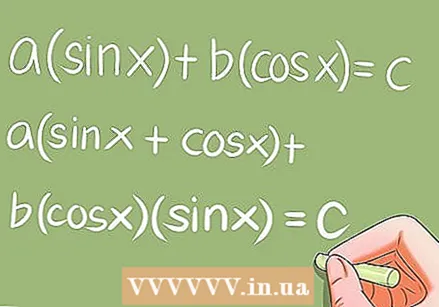7. לפתור משוואות טריגונומטריות מיוחדות.
   • יש כמה משוואות טריגונומטריות מיוחדות הדורשות המרות ספציפיות. דוגמאות:
   • a * sin x + b * cos x = c; a (sin x + cos x) + b * cos x * sin x = c;
   • a * * sin ^ 2 x + b * sin x * cos x + c * cos ^ 2 x = 0
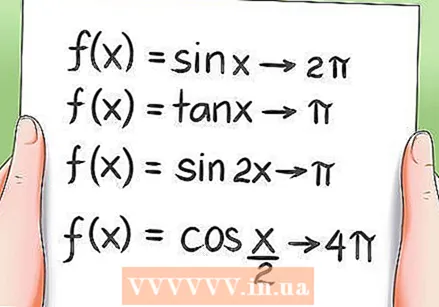8. למד את המאפיינים התקופתיים של פונקציות טריגונומטריות.
   • כל הפונקציות הטריגונומטריות הן תקופתיות, כלומר הן חוזרות לאותו ערך לאחר סיבוב על פני תקופה. דוגמאות:
     • לפונקציה f (x) = sin x יש 2Pi כתקופה.
     • לפונקציה f (x) = שיזוף x יש את Pi כתקופה.
     • לפונקציה f (x) = sin 2x יש את Pi כנקודה.
     • לפונקציה f (x) = cos (x / 2) יש 4Pi כתקופה.
   • אם הנקודה מוגדרת בתרגילים / במבחן, אתה רק צריך למצוא את העקומה (ים) x בתוך תקופה זו.
   • הערה: פתרון משוואות טריגונומטריות הוא מסובך ולעתים קרובות מוביל לשגיאות וטעויות. לכן יש לבדוק היטב את התשובות. לאחר הפתרון, תוכלו לבדוק את התשובות באמצעות מחשבון גרפי, לייצוג ישיר של המשוואה הטריגונומטרית הנתונה R (x) = 0. התשובות (כשורש ריבועי) ניתנות במקומות עשרוניים. כדוגמה, לפי יש ערך של 3.14