תוֹכֶן

• לדרוך
• חלק 1 מתוך 4: שרטוט המטריצה
• חלק 2 מתוך 4: לימוד הפעולות לפתרון מערכת עם מטריצה
• חלק 3 מתוך 4: מיזג את השלבים לפתרון הגלקסיה
• חלק 4 מתוך 4: בדיקת הפיתרון שלך
• טיפים

מטריצה ​​היא דרך שימושית מאוד לייצג מספרים בתבנית בלוק, שבה תוכלו להשתמש כדי לפתור מערכת של משוואות ליניאריות. אם יש לך רק שני משתנים, סביר להניח שתשתמש בשיטה אחרת. קרא על כך בפתרון מערכת משוואות לדוגמאות לשיטות אחרות אלה. אך אם יש לך שלושה משתנים או יותר, מערך הוא אידיאלי. על ידי שימוש בשילובים חוזרים של כפל והוספה ניתן להגיע באופן שיטתי לפיתרון.

לדרוך

חלק 1 מתוך 4: שרטוט המטריצה

1. ודא שיש לך מספיק נתונים. כדי לקבל פיתרון ייחודי לכל משתנה במערכת ליניארית באמצעות מטריצה, עליך להיות בעל משוואות רבות ככל מספר המשתנים שאתה מנסה לפתור. לדוגמא: עם המשתנים x, y ו- z אתה זקוק לשלוש משוואות. אם יש לך ארבעה משתנים, אתה זקוק לארבע משוואות.
   • אם יש לך פחות משוואות ממספר המשתנים, תגלה כמה גבולות של המשתנים (כגון x = 3y ו- y = 2z), אך אינך יכול לקבל פתרון מדויק. למאמר זה נעבוד רק לפיתרון ייחודי.
2. כתוב את המשוואות שלך בצורה סטנדרטית. לפני שתוכל לשים נתונים מהמשוואות בצורה של מטריצה, תחילה אתה כותב כל משוואה בצורה סטנדרטית. הצורה הסטנדרטית למשוואה ליניארית היא Ax + By + Cz = D, כאשר האותיות הגדולות הן המקדמים (מספרים), והמספר האחרון (D בדוגמה זו) נמצא מימין לסימן השווה.
   • אם יש לך יותר משתנים, פשוט המשך את הקו כל עוד אתה צריך. לדוגמא, אם ניסית לפתור מערכת עם שישה משתנים, צורת ברירת המחדל שלך תיראה כמו Au + Bv + Cw + Dx + Ey + Fz = G. במאמר זה נתמקד במערכות עם שלושה משתנים בלבד. פתרון גלקסיה גדולה יותר זהה לחלוטין, אך פשוט לוקח יותר זמן ויותר צעדים.
   • שימו לב שבצורה סטנדרטית, הפעולות בין התנאים הן תמיד תוספת. אם יש חיסור במשוואה שלך, במקום תוספת, תצטרך לעבוד עם זה בהמשך על ידי הפיכת המקדם שלך לשלילי. כדי להקל על הזיכרון, ניתן לשכתב את המשוואה ולהוסיף את הפעולה ולהפוך את המקדם לשלילי. לדוגמא, תוכל לשכתב את המשוואה 3x-2y + 4z = 1 כ- 3x + (- 2y) + 4z = 1.
3. מקם את המספרים ממערכת המשוואות במטריצה. מטריצה ​​היא קבוצת מספרים, המסודרים במעין טבלה, איתה נעבוד לפתרון המערכת. הוא מכיל בעצם את אותם נתונים כמו המשוואות עצמן, אך בפורמט פשוט יותר. כדי להפוך את המטריצה ​​של המשוואות שלך בצורה סטנדרטית, פשוט העתק את המקדמים והתוצאה של כל משוואה לשורה אחת, וערם את השורות האלה זו על גבי זו.
   • נניח שיש לך מערכת המורכבת משלוש המשוואות 3x + y-z = 9, 2x-2y + z = -3 ו- x + y + z = 7. השורה העליונה של המטריצה ​​שלך תכיל את המספרים 3, 1, -1, 9, שכן אלה המקדמים והפתרון של המשוואה הראשונה. שימו לב כי כל משתנה שאין לו מקדם מניח שיש לו מקדם 1. השורה השנייה של המטריצה ​​הופכת ל -2, -2, 1, -3 והשורה השלישית הופכת ל -1, 1, 1, 7.
   • הקפד ליישר את מקדמי x בעמודה הראשונה, מקדמי y בשני, מקדמי z בשלישי, ומונחי הפתרון ברביעי. לאחר שתסיים לעבוד עם המטריצה, העמודות הללו יהיו חשובות בעת כתיבת הפתרון שלך.
4. צייר סוגר מרובע גדול סביב כל המטריצה ​​שלך. לפי מוסכמות, מטריצה ​​מסומנת על ידי זוג סוגריים מרובעים, [], סביב כל גוש המספרים. הסוגריים אינם משפיעים על הפתרון בשום צורה שהיא, אך הם מצביעים על כך שאתה עובד עם מטריצות. מטריצה ​​יכולה להיות מורכבת מכל מספר שורות ועמודות. במאמר זה נשתמש בסוגריים סביב מונחים ברצף כדי לציין שהם שייכים זה לזה.
5. שימוש בסמליות נפוצה. כאשר עובדים עם מטריצות, נהוג להתייחס לשורות עם קיצור R ולעמודות עם קיצור C. ניתן להשתמש במספרים יחד עם אותיות אלה כדי לציין שורה או עמודה ספציפיים. לדוגמה, כדי לציין שורה 1 של מטריצה, אתה יכול לכתוב R1. שורה 2 הופכת לאחר מכן ל- R2.
   • אתה יכול לציין כל מיקום ספציפי במטריצה ​​באמצעות שילוב של R ו- C. לדוגמה, כדי לציין מונח בשורה השנייה, בעמודה השלישית, אתה יכול לקרוא לזה R2C3.

חלק 2 מתוך 4: לימוד הפעולות לפתרון מערכת עם מטריצה

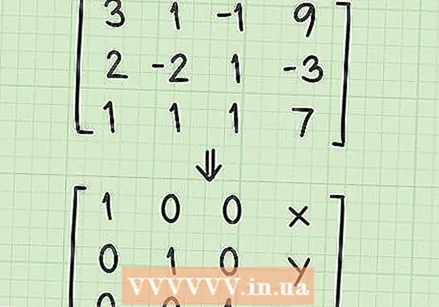1. להבין את הצורה של מטריצת הפתרון. לפני שתתחיל לפתור את מערכת המשוואות שלך, עליך להבין מה אתה הולך לעשות עם המטריצה. בשלב זה יש לך מטריצה ​​שנראית כך:
   • 3 1 -1 9
   • 2 -2 1 -3
   • 1 1 1 7
   • אתה עובד עם מספר פעולות בסיסיות ליצירת "מטריצת הפיתרון". מטריצת הפיתרון תיראה כך:
   • 1 0 0 x
   • 0 1 0 y
   • 0 0 1 z
   • שימו לב שהמטריצה ​​מורכבת מ -1 בקו אלכסוני עם 0 בכל שאר הרווחים למעט העמודה הרביעית. המספרים בעמודה הרביעית הם הפתרון למשתנים x, y ו- z.
2. השתמש בכפל סקלרי. הכלי הראשון שעומד לרשותך לפתרון מערכת באמצעות מטריצה ​​הוא כפל סקלרי. זה פשוט מונח שמשמעותו שאתה מכפיל את האלמנטים בשורה של המטריצה ​​במספר קבוע (לא משתנה). בעת שימוש בכפל סקלרי, זכור כי עליך להכפיל כל מונח של כל השורה במספר שתבחר. אם תשכח את הקדנציה הראשונה ופשוט תכפיל, תקבל את הפיתרון הלא נכון. עם זאת, אינך צריך להכפיל את כל המטריצה ​​בו זמנית. בכפל סקלרי, אתה עובד רק על שורה אחת בכל פעם.
   • מקובל להשתמש בשברים בכפל סקלרי מכיוון שלעתים קרובות רוצים לקבל שורה אלכסונית של 1. להתרגל לעבוד עם שברים. זה יהיה קל יותר (ברוב השלבים לפתרון המטריצה) להיות מסוגל לכתוב את השברים שלך בצורה לא נכונה, ואז להמיר אותם בחזרה למספרים מעורבים לפתרון הסופי. לכן, המספר 1 2/3 קל יותר לעבוד איתו אם כותבים אותו כ- 5/3.
   • לדוגמה, השורה הראשונה (R1) של בעיית הדוגמה שלנו מתחילה במונחים [3,1, -1,9]. מטריצת הפתרון חייבת להכיל 1 במיקום הראשון בשורה הראשונה. כדי "לשנות" את ה- 3 ל- 1, נוכל להכפיל את השורה כולה ב- 1/3. זה יוצר את ה- R1 החדש של [1,1 / 3, -1 / 3,3].
   • דאג להשאיר כל סימן שלילי במקום בו הם שייכים.
3. השתמש בתוספת שורה או חיסור בשורה. הכלי השני שבו אתה יכול להשתמש הוא להוסיף או לחסר שתי שורות של המטריצה. כדי ליצור את 0 המונחים במטריצת הפתרונות שלך, עליך להוסיף או לחסר מספרים כדי להגיע ל 0. לדוגמא, אם R1 הוא מטריצה ​​[1,4,3,2] ו- R2 הוא [1,3,5,8], אז תוכל להפחית את השורה הראשונה מהשורה השנייה וליצור שורה חדשה [0, -1, 2.6], כי 1-1 = 0 (עמודה ראשונה), 3-4 = -1 (עמודה שנייה), 5-3 = 2 (עמודה שלישית) ו- 8-2 = 6 (עמודה רביעית). בעת ביצוע תוספת שורה או חיסור שורה, כתוב מחדש את התוצאה החדשה שלך במקום השורה איתה התחלת. במקרה זה נחלץ את שורה 2 ונכניס את השורה החדשה [0, -1,2,6].
   • אתה יכול להשתמש בסימון קצרנות ולהצהיר על פעולה זו כ- R2-R1 = [0, -1,2,6].
   • זכור שחיבור וחיסור הם צורות הפוכות בדיוק לאותה פעולה. חשוב על זה להוסיף שני מספרים או להפחית את ההפך. לדוגמא, אם אתה מתחיל במשוואה הפשוטה 3-3 = 0, אתה יכול לחשוב על זה כעל בעיית תוספת של 3 + (- 3) = 0. התוצאה זהה. זה נראה פשוט, אך לפעמים קל יותר לשקול בעיה בצורה כזו או אחרת. רק לפקוח עין על הסימנים השליליים שלך.
4. שלב תוספת שורה וכפל סקלרי בשלב אחד. אינך יכול לצפות שהתנאים יתאימו תמיד, כך שתוכל להשתמש בתוספת פשוטה או בחיסור כדי ליצור 0 במטריקס שלך. לעתים קרובות יותר תצטרך להוסיף (או לחסר) מכפלה משורה אחרת. לשם כך, תחילה בצע את הכפל הסקלרי, ואז הוסף את התוצאה לשורת היעד שאתה מנסה לשנות.
   • לְהַנִיחַ; שיש שורה 1 של [1,1,2,6] ושורה 2 של [2,3,1,1]. אתה רוצה מונח 0 בעמודה הראשונה של R2. כלומר, אתה רוצה לשנות את ה- 2 ל- 0. כדי לעשות זאת, עליך להפחית את ה- 2. אתה יכול לקבל 2 על ידי הכפלת שורה 1 בכפל הסקלרי 2, ולאחר מכן הפחתת השורה הראשונה מהשורה השנייה. בצורה קצרה ניתן לרשום את זה כ- R2-2 * R1. ראשית, הכפל את R1 בשני כדי לקבל [2,2,4,12]. לאחר מכן חיסר זאת מ- R2 כדי לקבל [(2-2), (3-2), (1-4), (1-12)]. פשוט את זה וה- R2 החדש שלך יהיה [0,1, -3, -11].
5. העתק שורות שנותרו ללא שינוי בזמן שאתה עובד. תוך כדי עבודה על המטריצה, תשנה שורה אחת בכל פעם, על ידי כפל סקלרי, הוספת שורה, או חיסור שורה, או שילוב של צעדים. כשאתה משנה שורה אחת, הקפד להעתיק את השורות האחרות של המטריצה ​​שלך בצורה המקורית שלהן.
   • שגיאה נפוצה מתרחשת בעת ביצוע שלב כפל והוספה משולב במהלך אחד. לדוגמא, נניח שעליך להפחית פעמיים מ- R1 מ- R2. כאשר מכפילים R1 ב -2 כדי לבצע את הצעד הזה, זכרו כי R1 אינו משתנה במטריצה. אתה עושה את הכפל רק כדי לשנות את R2. העתק תחילה את R1 בצורתו המקורית ואז בצע את השינוי ל- R2.
6. עבודה ראשונה מלמעלה למטה. כדי לפתור את המערכת, אתה עובד בתבנית מסודרת מאוד, ובעצם "פותר" מונח אחד בכל פעם מהמטריקס. הרצף של מערך בן שלושה משתנים ייראה כך:
   • 1. הכינו 1 בשורה הראשונה, העמודה הראשונה (R1C1).
   • 2. הפוך 0 בשורה השנייה, העמודה הראשונה (R2C1).
   • 3. הכינו 1 בשורה השנייה, העמודה השנייה (R2C2).
   • 4. הפוך 0 בשורה השלישית, העמודה הראשונה (R3C1).
   • 5. הפוך 0 בשורה השלישית, העמודה השנייה (R3C2).
   • 6. הכינו 1 בשורה השלישית, בעמודה השלישית (R3C3).
7. עבודה חזרה מלמטה למעלה. בשלב זה, אם ביצעת את השלבים בצורה נכונה, אתה נמצא באמצע הדרך לפתרון. אתה חייב להיות עם הקו האלכסוני של 1, ומתחתו 0. המספרים בעמודה הרביעית אינם חשובים בשלב זה. עכשיו אתה עובד חזרה לראש הדף באופן הבא:
   • צור 0 בשורה השנייה, העמודה השלישית (R2C3).
   • צור 0 בשורה הראשונה, העמודה השלישית (R1C3).
   • צור 0 בשורה הראשונה, העמודה השנייה (R1C2).
8. בדוק אם יצרת את מטריצת הפתרון. אם העבודה שלך נכונה, יצרת את מטריצת הפיתרון עם 1 בשורה אלכסונית של R1C1, R2C2, R3C3 ו- 0 במיקומים האחרים של שלוש העמודות הראשונות. המספרים בעמודה הרביעית הם הפתרונות למערכת הליניארית שלך.

חלק 3 מתוך 4: מיזג את השלבים לפתרון הגלקסיה

1. התחל במערכת דוגמה של משוואות ליניאריות. כדי לתרגל שלבים אלה, נתחיל מהמערכת בה השתמשנו קודם: 3x + y-z = 9, 2x-2y + z = -3 ו- x + y + z = 7. אם אתה כותב זאת במטריצה, יש לך R1 = [3,1, -1,9], R2 = [2, -2,1, -3] ו- R3 = [1,1,1,7].
2. צור 1 במיקום הראשון R1C1. שים לב ש- R1 מתחיל בנקודה זו בשלב 3. אתה צריך לשנות אותו ל- 1. אתה יכול לעשות זאת על ידי כפל סקלרי, ומכפיל את כל ארבעת המונחים של R1 ב 1/3. בקיצור אתה יכול לכתוב כ R1 * 1/3. זה נותן תוצאה חדשה עבור R1 אם R1 = [1,1 / 3, -1 / 3,3]. העתק R2 ו- R2, ללא שינוי, כאשר R2 = [2, -2,1, -3] ו- R3 = [1,1,1,7].
   • שים לב שכפל וחילוק הם פונקציות הפוכות בלבד זו מזו. אנו יכולים לומר שאנחנו מכפילים ב- 1/3 או מחלקים ב- 3, מבלי לשנות את התוצאה.
3. צור 0 בשורה השנייה, העמודה הראשונה (R2C1). בשלב זה, R2 = [2, -2,1, -3]. כדי להתקרב למטריצת הפתרונות, עליך לשנות את המונח הראשון מ- 2 ל- 0. אתה יכול לעשות זאת על ידי חיסור כפול מהערך R1, מכיוון ש- R1 מתחיל ב- 1. בקיצור, הפעולה R2- 2 * R1. זכרו, אתם לא מחליפים R1, פשוט עובדים איתו. אז העתק ראשון R1 אם R1 = [1,1 / 3, -1 / 3,3]. ואז אם מכפילים כל מונח של R1, מקבלים 2 * R1 = [2,2 / 3, -2 / 3,6]. לבסוף, הפחיתו תוצאה זו מה- R2 המקורי כדי לקבל את ה- R2 החדש שלכם. עבודה מונח אחר מונח, חיסור זה הופך להיות (2-2), (-2-2 / 3), (1 - (- 2/3)), (-3-6). אנו מפשטים אותם ל- R2 החדש [[0, -8 / 3,5 / 3, -9]. שים לב כי הקדנציה הראשונה היא 0 (תהיה מטרתך אשר תהיה).
   • כתוב שורה 3 (שלא השתנתה) כ- R3 = [1,1,1,7].
   • היזהר בעת חיסור מספרים שליליים כדי לוודא שהסימנים נשארים תקינים.
   • עכשיו ראשית בואו נעזוב את השברים בצורתם הלא נכונה. זה מקל על השלבים המאוחרים יותר של הפתרון. אתה יכול לפשט את השברים בשלב האחרון של הבעיה.
4. צור 1 בשורה השנייה, העמודה השנייה (R2C2). כדי להמשיך ליצור את הקו האלכסוני של 1, עליך להמיר את המונח השני -8/3 ל -1. עשו זאת על ידי הכפלת כל השורה בגומלין המספר הזה (-3/8). באופן סמלי, שלב זה הוא R2 * (- 3/8). השורה השנייה המתקבלת היא R2 = [0.1, -5 / 8.27 / 8].
   • שים לב שאם המחצית השמאלית של השורה תתחיל להידמות לפיתרון עם ה- 0 וה -1, המחצית הימנית עשויה להתחיל להראות מכוערת, עם שברים לא תקינים. פשוט השאר אותם למה שהם בינתיים.
   • אל תשכח להמשיך להעתיק את השורות שלא נגעו בהן, לכן R1 = [1,1 / 3, -1 / 3,3] ו- R3 = [1,1,1,7].
5. צור 0 בשורה השלישית, העמודה הראשונה (R3C1). המיקוד שלך עובר כעת לשורה השלישית, R3 = [1,1,1,7]. כדי לבצע 0 במיקום הראשון, עליך להפחית 1 מה- 1 שנמצא במיקום זה. אם אתה מסתכל למעלה, יש 1 במיקום הראשון של R1. אז אתה רק צריך להפחית R1 מ R3 כדי לקבל את התוצאה שאתה צריך. מונח עבודה למונח, זה הופך להיות (1-1), (1-1 / 3), (1 - (- 1/3)), (7-3). לאחר מכן ניתן לפשט את ארבע מיני הבעיות הללו ל- R3 החדש [0.2 / 3.4 / 3.4].
   • המשך להעתיק לאורך R1 = [1.1 / 3, -1 / 3.3] ו- R2 = [0.1, -5 / 8.27 / 8]. זכור שאתה משנה רק שורה אחת בכל פעם.
6. בצע 0 בשורה השלישית, העמודה השנייה (R3C2). ערך זה כרגע הוא 2/3, אך עליו להמיר אותו ל- 0. במבט ראשון נראה כי ניתן לחסר את ערכי R1 בכפול, מכיוון שהעמודה המקבילה של R1 מכילה 1/3. עם זאת, אם מכפילים ומחסירים את כל הערכים של R1, 0 בעמודה הראשונה של R3 משתנה, מה שאתה לא רוצה. זה יהיה צעד אחורה בפתרון שלך. אז אתה צריך לעבוד עם שילוב כלשהו של R2. הפחתת 2/3 מ- R2 יוצרת 0 בעמודה השנייה, מבלי לשנות את העמודה הראשונה. בצורה קצרה זהו R3-2 / 3 * R2. המונחים האישיים הופכים להיות (0-0), (2 / 3-2 / 3), (4/3 - (- 5/3 * 2/3)), (4-27 / 8 * 2/3) . הפשט ואז נותן R3 = [0,0,42 / 24,42 / 24].
7. צור 1 בשורה השלישית, בעמודה השלישית (R3C3). זהו כפל פשוט לפי הדדי המספר שאומר. הערך הנוכחי הוא 42/24, כך שתוכל להכפיל ב 24/42 כדי לקבל את הערך הרצוי 1. שימו לב ששני המונחים הראשונים הם שניהם, כך שכל כפל נשאר 0. הערך החדש של R3 = [0,0,1,1].
   • שים לב שהשברים שנראו די מורכבים בשלב הקודם כבר מתחילים להיפתר.
   • המשך עם R1 = [1.1 / 3, -1 / 3.3] ו- R2 = [0.1, -5 / 8.27 / 8].
   • שים לב שבשלב זה יש לך את האלכסון של 1 למטריצת הפתרונות שלך. אתה רק צריך להמיר שלושה אלמנטים של המטריצה ​​ל- 0 כדי למצוא את הפתרון שלך.
8. צור 0 בשורה השנייה, בעמודה השלישית. R2 כרגע הוא [0.1, -5 / 8.27 / 8], עם הערך -5/8 בעמודה השלישית. אתה צריך להפוך אותו ל- 0. זה אומר שאתה צריך לבצע פעולה כלשהי עם R3 שמורכבת מהוספת 5/8. מכיוון שהעמודה השלישית המקבילה של R3 היא 1, עליכם להכפיל את כל הערכים של R3 ב- 5/8 ולהוסיף את התוצאה ל- R2. בקיצור זה R2 + 5/8 * R3. מונח למונח זה הוא R2 = (0 + 0), (1 + 0), (-5 / 8 + 5/8), (27/8 + 5/8). ניתן לפשט זאת ל- R2 = [0,1,0,4].
   • לאחר מכן העתק R1 = [1,1 / 3, -1 / 3,3] ו- R3 = [0,0,1,1].
9. צור 0 בשורה הראשונה, בעמודה השלישית (R1C3). השורה הראשונה כרגע היא R1 = [1,1 / 3, -1 / 3,3]. עליך להמיר את -1/3 בעמודה השלישית ל- 0, באמצעות שילוב כלשהו של R3. אינך רוצה להשתמש ב- R2 מכיוון שה- 1 בעמודה השנייה של R2 ישנה את R1 בצורה לא נכונה. אז מכפילים R3 * 1/3 ומוסיפים את התוצאה ל- R1. הסימון לכך הוא R1 + 1/3 * R3. המונח לעיבוד מונחים מביא ל- R1 = (1 + 0), (1/3 + 0), (-1 / 3 + 1/3), (3 + 1/3). אתה יכול לפשט את זה ל- R1 חדש [1,1 / 3,0,10 / 3].
   • העתק את ה- R2 ללא שינוי = [0,1,0,4] ו- R3 = [0,0,1,1].
10. בצע 0 בשורה הראשונה, העמודה השנייה (R1C2). אם הכל נעשה נכון, זה אמור להיות השלב האחרון. אתה צריך להמיר 1/3 בעמודה השנייה ל- 0. אתה יכול להשיג זאת על ידי הכפלת והפחתת R2 * 1/3. בקצרה, זה R1-1 / 3 * R2. התוצאה היא R1 = (1-0), (1 / 3-1 / 3), (0-0), (10 / 3-4 / 3). הפשט ואז נותן R1 = [1,0,0,2].
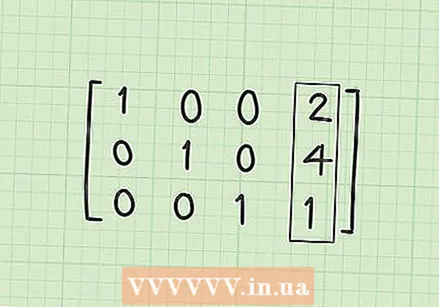11. חפש את מטריצת הפתרון. בשלב זה, אם הכל ילך כשורה, יהיו לך שלוש השורות R1 = [1,0,0,2], R2 = [0,1,0,4] ו- R3 = [0,0,1,1] חייב שיהיה לי. שים לב שאם אתה כותב את זה בצורה של מטריצת הבלוק עם השורות אחת מעל השנייה, יש לך אלכסונים 1 עם 0 יותר, והפתרונות שלך נמצאים בעמודה הרביעית. מטריצת הפיתרון צריכה להיראות כך:
    • 1 0 0 2
    • 0 1 0 4
    • 0 0 1 1
12. הבנת הפיתרון שלך. לאחר המרת המשוואות הלינאריות למטריצה, שמים את מקדמי x בעמודה הראשונה, מקדמי y בעמודה השנייה, מקדמי z בעמודה השלישית. אם ברצונך לשכתב את המטריצה ​​למשוואות שוב, שלוש השורות הללו של המטריצה ​​פירושן למעשה שלוש המשוואות 1x + 0y + 0z = 2, 0x + 1y + 0z = 4 ו- 0x + 0y + 1z = 1. מכיוון שנוכל לחצות את המונחים 0 ולא נצטרך לכתוב את המקדמים 1, שלוש המשוואות הללו מפשטות את הפיתרון, x = 2, y = 4 ו- z = 1. זה הפיתרון למערכת המשוואות הליניאריות שלך.

חלק 4 מתוך 4: בדיקת הפיתרון שלך

1. כלול את הפתרונות בכל משתנה בכל משוואה. זה תמיד רעיון טוב לבדוק שהפתרון שלך אכן נכון. אתה עושה זאת על ידי בדיקת התוצאות שלך במשוואות המקוריות.
   • המשוואות המקוריות לבעיה זו היו: 3x + y-z = 9, 2x-2y + z = -3 ו- x + y + z = 7. כשאתה מחליף את המשתנים בערכים שלהם שמצאת, תקבל 3 * 2 + 4-1 = 9, 2 * 2-2 * 4 + 1 = -3, ו- 2 + 4 + 1 = 7.
2. לפשט כל השוואה. בצע את הפעולות בכל משוואה על פי הכללים הבסיסיים של הפעולות. המשוואה הראשונה מפשטת ל 6 + 4-1 = 9, או 9 = 9. ניתן לפשט את המשוואה השנייה ל 4-8 + 1 = -3, או -3 = -3. המשוואה האחרונה היא פשוט 7 = 7.
   • מכיוון שכל משוואה מפשטת להצהרת מתמטיקה אמיתית, הפתרונות שלך נכונים. אם אחד הפתרונות שגויים, בדוק שוב את עבודתך וחפש שגיאות כלשהן. כמה טעויות נפוצות מתרחשות כאשר נפטרים מסימני מינוס בדרך או מבלבלים בין הכפל ותוספת השברים.
3. כתוב את הפתרונות הסופיים שלך. לבעיה נתונה זו, הפתרון הסופי הוא x = 2, y = 4 ו- z = 1.

טיפים

• אם מערכת המשוואות שלך מורכבת מאוד, עם הרבה משתנים, ייתכן שתוכל להשתמש במחשבון גרפים במקום לבצע את העבודה ביד. למידע על כך תוכלו גם להתייעץ עם wikiHow.